Calculating a NW Segment of Salem’s Class D Air Space

I’m still working on the matter of the low flying Learjet over Salem, and in that matter, I have determined the jet first flew parallel to the FAA’s Class D airspace as much as it could before entering it.

So then I wondered, why and what distance is involved. So here is a picture of the FAA’s Class D air space over Salem. It encompasses about 78 square miles. I asked ChatGPT for a strategy on how to determine the distance of the segment and it assumed I could easily determine the coordinates of the interior and exterior corner of the shape using a mouse over a map. I’m not thrilled with using a mouse over a map to obtain accurate coordinates, so I suggested we determine the points programmatically (through programming) and then I would have dead-accurate numbers — something the FAA and government might be comfortable with.

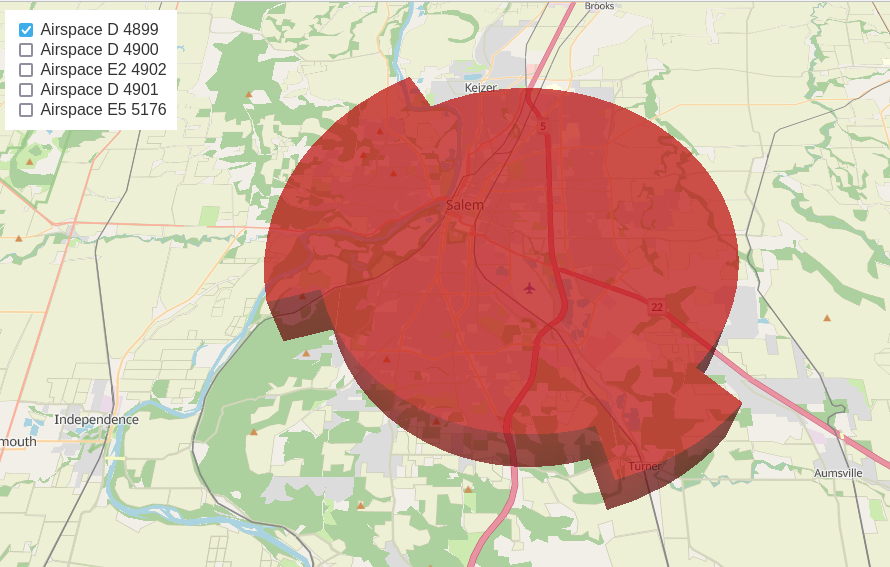
The top most straight line segment point at the northwest (pointing towards 11 o’clock) is the border that the Learjet flew along. I wanted to know what that segment’s distance is. So with the help of ChatGPT, we constructed a query that visits the 6,000+ points used to define the air space shape above and determine for any given 3 points, what the angle is. Then only those angles far away from 180 degrees (3 points in a straight line would have an angle of 180 degrees) or thereabout would be of interest and most likely represent corners.

nenrad=# WITH dumped_points AS (
SELECT (ST_DumpPoints(geom)).path[1] AS path,
(ST_DumpPoints(geom)).geom AS dumppoint
FROM air_space
WHERE gid = 4899
),
numbered_points AS (
SELECT dumppoint,
ROW_NUMBER() OVER (ORDER BY path) AS rn
FROM dumped_points
),
angles AS (
SELECT
p1.rn AS set_number,
ST_X(p1.dumppoint) AS lon1, ST_Y(p1.dumppoint) AS lat1,
ST_X(p2.dumppoint) AS lon2, ST_Y(p2.dumppoint) AS lat2,
ST_X(p3.dumppoint) AS lon3, ST_Y(p3.dumppoint) AS lat3,
DEGREES(ST_Angle(p1.dumppoint, p2.dumppoint, p3.dumppoint)) AS angle_degrees
FROM numbered_points p1
JOIN numbered_points p2 ON p2.rn = p1.rn + 1
JOIN numbered_points p3 ON p3.rn = p1.rn + 2
)
SELECT * FROM angles
WHERE angle_degrees < 150
or angle_degrees > 200
ORDER BY set_number;
set_number |       lon1        |       lat1       |       lon2        |       lat2       |       lon3        |       lat3       |   angle_degrees
------------+-------------------+------------------+-------------------+------------------+-------------------+------------------+--------------------
1 | -123.049964745861 | 44.9677836638676 | -123.049464768662 | 44.9671697198823 |  -123.04943115166 | 44.9671835198864 |  106.8398394614957
2848 | -122.933944159422 | 44.8639806424676 | -122.933962591422 | 44.8639666144649 | -122.933233883214 | 44.8634825285096 |  70.86996257022534
2858 |  -122.91866256406 | 44.8537998004016 | -122.916841492541 |  44.852589327513 | -122.916921516541 | 44.8525284755014 | 289.13771073176343
3400 | -122.970232557107 | 44.8293479767846 | -122.970238418108 | 44.8293467827839 |  -122.97092421055 | 44.8310512098155 | 259.59684676121486
3410 | -122.976412000093 | 44.8446864590673 |  -122.97668646527 | 44.8453682200799 | -122.976745919277 | 44.8453561140732 | 100.41965248870801
4982 | -123.092654881048 | 44.8910313170972 |  -123.09265841005 | 44.8910400430973 | -123.093617088157 | 44.8908438169895 | 100.45182726945418
4992 | -123.112789106295 | 44.8869174938315 | -123.115185425562 | 44.8864264775618 | -123.115217833583 | 44.8865065555632 | 259.54640914412636
6319 | -123.061262823349 | 44.9815778035296 | -123.061217070346 | 44.9815965915353 | -123.059966544847 | 44.9800618785723 | 253.15093018349765
(8 rows)

nenrad=#

ChatGPT then created an HTML page displaying a map showing where the 8 points appear on the map as I told it that I wanted to verify visually the above calculations. Bingo: an HTML page showing me the points.

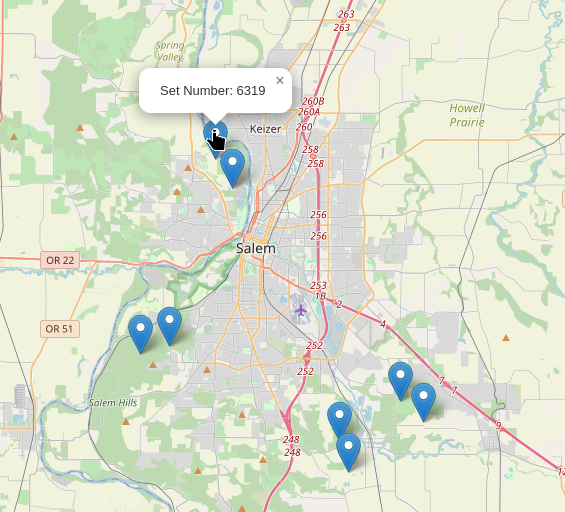
Then I took the middle coordinates, “lon2” & “lat2”, for set #1 and set #6319 and computed the distance:

nenrad=# SELECT ST_Distance(
ST_Transform(ST_GeomFromText('POINT(-123.049464768662 44.9671697198823)', 4326), 3210),
ST_Transform(ST_GeomFromText('POINT(-123.061217070346 44.9815965915353)', 4326), 3210)
) AS distance_meters;
distance_meters
------------------
9710.43676387841
(1 row)

nenrad=#

9710 meters which is about 6 miles.

Having fun with ChatGPT and FAA air space shapes!